Afin d’obtenir une réponse compétente à la question de titre, le lecteur de l’article devra faire l’objet d’une réflexion approfondie sur ses capacités de pensée abstraite et sur la manière d’approfondir certaines parties des mathématiques enseignées à l’école. Et pour stimuler l’imagination, il sera utile de rappeler que «l’éducation est ce qui reste après que l’on oublie tout ce qui nous a été enseigné» (l’auteur de la phrase est attribué à A. Einstein).
Une légère immersion dans l'une des sections de mathématiques
Pour commencer, il sera nécessaire de rappeler l’existence de la science de la géométrie (ce mot signifie «mesure du sol») - une branche distincte des mathématiques spécialisées dans l’étude des structures spatiales, de leurs relations réciproques et des diverses généralisations qui en découlent. Il est important que, malgré l’origine similaire «surnommée» du nom, cette science fonctionne avec des concepts purement abstraits qui, dans le monde familier, n’existent pas en incarnation physique directe.
L'un de ces concepts de base estle point géométrique . Tendez votre imagination: contrairement à “une pointe de crayon”, “un point d’épingle” et ainsi de suite, ce point est un objet totalement abstrait dans un espace imaginaire sans caractéristiques mesurables comme “l’épaisseur”, la “couleur”, etc. ils aiment prononcer l'expression «objet de dimension zéro»). En principe, tout le reste de la géométrie sera déterminé plus avant sur la base de cette abstraction.

Ce qui suit est nécessaire pour approfondir le concept - il s’agit d’une expression mathématique "rituelle" "lieu géométrique de points" (HMT). Avec son aide, un certain ensemble de points tombant sous une certaine relation est décrit - voici comment est définie une «figure géométrique». Exemple: une sphère (du grec ancien σφαῖρα, désignant à l’origine une balle /balle) est un lieu géométrique de tels points de l’espace qui peut être décrit comme étant à égale distance (situé exactement à une distance) d’un point donné, généralement appelé "centre de la sphère".
sphère
La distance entre le centre de la sphère et ce GMT est appelée le «rayon de la sphère». Au cours de toutes ces manipulations, il est important de garder à l’esprit que la sphère est un concept plus éphémère que même une bulle familière et familière: même une bulle de savon possède une paroi bien tangible d’un film eau-savon d’épaisseur microscopique qui peut être mesurée physiquement même percer), et la sphère - non!

Sphère et rayon de la sphère
Passons maintenant à la définition d'une balle: une balle est une collection de tous ces points d'espace situés à partir d'un certain point (centre de la balle) à une distance ne dépassant pas un point donné (rayon de la balle). En d’autres termes, une balle est un "corps géométrique" - en ce sens que, selon la définition principale d’Euclide, "a la longueur, la largeur et la profondeur" (dans les manuels modernes, cette définition est moins claire): "une partie de l’espace limité par ses propresforme ").
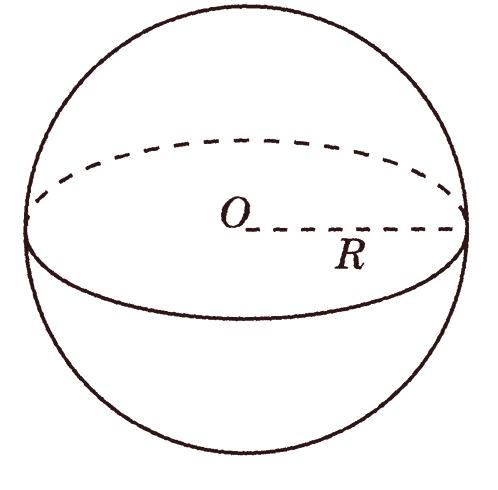
Shar
Dans le même temps, nous notons que les méthodes utilisées pour spécifier une sphère et une balle par le centre et le rayon utilisés ici ne sont pas les seules: par exemple, la définition d’une sphère /balle dans l’espace peut être réalisée en faisant pivoter un cercle, un cercle, etc. (Intéressé profondément à cette question, il est fortement recommandé de se familiariser avec une section distincte de la géométrie appelée "Formes et corps de révolution", car il s'agit d'un moyen fréquemment utilisé pour définir les formes et corps géométriques les plus divers dans l'espace).
Ainsi, dans le cas d’une sphère et dans le cas d’une balle, il faut tenir compte d’une certaine manière du lieu géométrique des points (c’est-à-dire d’une figure géométrique), mais on ne peut parler d’un corps géométrique que dans le cas d’une balle. Il est curieux de noter que la sphère à proprement parler peut être «soustraite» de la sphère: dans ce cas, les mathématiciens parlent de «boule ouverte». Cependant, «par défaut», il existe une «boule fermée», où la sphère est sa limite naturelle et en fait partie.
Résumé
La boule et la sphère sont des objets géométriques abstraits (figures géométriques) définies par un certain lieu géométrique de points dans l’espace, par exemple en utilisant le concept de centre de la boule /sphère et le rayon de la boule /sphère. Cependant, seule la balle est un corps géométrique à part entière, car elle comprend non seulement la description de la surface qui la délimite, mais également la totalité de la surface de celle-ci. De ce point de vue, la sphère n'est qu'une frontière abstraite externe.(surface) de la balle définie dans l'espace.
Il est également important de se rappeler que seule la définition par défaut d'une «boule fermée» inclut cette limite; en cas d'exclusion, un corps géométrique entièrement nouveau est obtenu: la «boule ouverte».