Les gens ont commencé à utiliser des chiffres il y a longtemps. Pour cela, ils ont principalement utilisé les doigts de leurs mains. Les gens montraient simplement aux doigts le nombre d'objets qu'ils voulaient rapporter. Les noms des nombres sont donc apparus et progressivement consolidés: 1, 2, 3, 4, 5, 6, 7, 8, 9. Et si il y avait plus d'objets que de doigts? Ensuite, j'ai dû montrer mes mains plusieurs fois, ce qui, bien sûr, ne convenait pas à tout le monde. Et puis les hommes intelligents, en Inde ou dans le monde arabe, ont trouvé un autre nombre - zéro, ce qui signifie l'absence d'objets, et avec lui le système de nombres décimaux. La décimale est due au fait que dix nombres sont utilisés:0, 1, 2, 3, 4, 5, 6, 7, 8, 9 . 
Numérotation décimale et numérique
Les numéros diffèrent des nombres en ce quepeut consister en un ou plusieurs numéros enregistrés dans une rangée . Le système de nombre décimal est un système de position. La valeur d'un chiffre dépend de la place (position) qu'il occupe dans le nombre. Les nombres sont aussi des nombres, mais composés d'un chiffre, qui occupe une position dans la décharge des unités. Si vous avez besoin d'écrire le nombre suivant par ordre de 9, vous devez passer à la catégorie suivante - les dizaines.
Le prochain nombre sera donc 10 - un dix, zéro unités, 11 - un dix une unité, 12 - un dix deux unités, 25 - deux douzaine de cinq unités et ainsi de suite. Après le nombre 99 vient le nombre 100 - cent zéro douzaine d'unités zéro. Ensuite, les rangs de milliers, dizaines de milliers, centaines de milliers, millions, etc. sont ajoutés. Ainsi, en ajoutant de nouveaux rangs à gauche, nous pouvons utiliser de plus en plus degrand nombre.
Nombres fractionnaires
Depuis le recalcul des objets, effectué à l’aide de nombres naturels, l’humanité a naturellement procédé au comptage des mesures de longueur, de poids et de temps. Et puis il y avait un problème pour savoir comment compter les parties non intégrales. Les fractions naturelles sont apparues naturellement: moitié, troisième, quart, cinquième, etc. Ils ont commencé à écrire sous la forme du numérateur et du dénominateur: le dénominateur a été enregistré sur le nombre de parties, le nombre entier est divisé, et dans le numérateur - combien de parties sont prises. Par exemple, la moitié est 1/2, le tiers 1/3, le quart 1/4, etc.
fractions décimales
Étant donné que l’humanité a de plus en plus utilisé le système de nombres décimaux, réduire les enregistrements de nombres fractionnaires en nombres décimaux, les fractions ayant un dénominateur sous la forme d’unités de bits 10, 100, 1000, 10 000, etc. a commencé à écrire sous la forme de fractions décimales, la fraction étant séparée de la virgule ou du point. Par exemple, 1/10 = 0,1, 1/100 = 0,01, 1/1000 = 0,001, 1/10000 = 0,0001. De plus, les fractions conventionnelles ont commencé à être converties en nombres décimaux en divisant le numérateur par le dénominateur. Si le remplacement exact échouait, il était calculé approximativement, avec une précision qui répond aux besoins pratiques des utilisateurs. 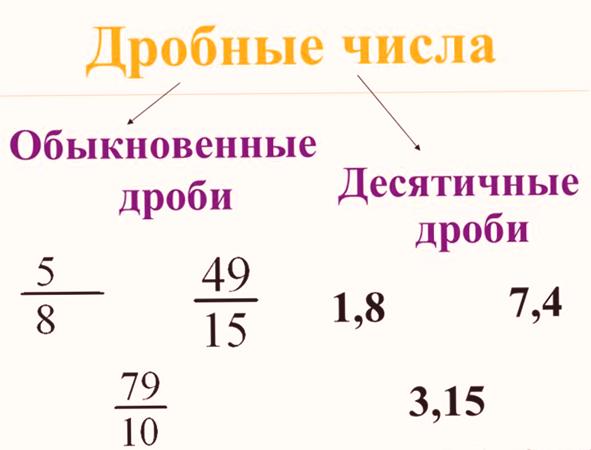
chiffres romains
Inutile de penser que le nombre décimal auquel nous sommes habitués, avec ses dix chiffres, a été utilisé partout et à tout moment. Par exemple, dans le célèbre empire romain, des nombres complètement différents ont été utilisés, qui servent parfois à numéroter des chapitres dans des livres, des désignations de siècles, etc. Ces chiffres que nous appelons romains et il n'y avait quesept: І - un, V - cinq, X - dix, L - cinquante, C - cent, D - cinq cents, M - mille. Avec l'aide de ces sept numéros, tous les autres numéros ont été enregistrés. Si un chiffre plus petit était placé devant un chiffre plus grand, il était ensuite soustrait du chiffre le plus grand, et si, après un chiffre plus grand, il était ajouté. Certains des mêmes numéros ne peuvent pas être répétés plus de trois fois de suite. Par exemple, II est deux, III est trois, IV est quatre (5 - 1 = 4), VI est six (5 + 1 = 6).
Autres systèmes de numération
Avec le début du développement de la technologie informatique, on a commencé à utiliser d'autres systèmes de numérotation, des machines plus proches que les personnes. Par exemple, Natural pour les ordinateurs est un système de nombres binaires composé de deux nombres: 0 et 1. Par exemple, nous écrivons plusieurs nombres à la suite en utilisant un système de nombres binaires: 0 = zéro, 1 = un, 10 deux (zéro et un deux) 11 - trois (une unité et un deux), 100 - quatre (zéro unité, zéro deux, un quatre), 101 - cinq (une unité, zéro deux, un quatre), etc. C'est-à-dire que les unités de bits ici sont deux fois différentes: deux, quatre, huit, etc.
Outre le système de numération binaire, les systèmes octal et hexadécimal sont maintenant largement utilisés en informatique et en programmation.