Aujourd'hui, le mot "Intégrale" peut être entendu assez souvent, et souvent dans les endroits les plus inattendus, par exemple sur la chaîne boursière à la télévision ou aux actualités. On entend souvent l'expression "indicateurs intégrés", le mot "intégré", "intégratif", etc. De manière générale, les responsables et les présentateurs de télévision sont généralement friands de divers termes à la mode, bien qu’ils aient peu de chance de comprendre leur véritable sens. Et aujourd'hui, nous allons parler de ce qu'est l'intégrale, quels types d'intégrale existent et quelles sont leurs différences.
Quelle est l'intégrale
Intégral est un mot latin qui nous vient de l’Antiquité et qui signifie «entier» ou «complet». C'est-à-dire qu'il est clair que si un objet était parlé d'un objet, par exemple d'un récipient en lait, cela signifiait qu'il était plein et combien de lait y était contenu, il en restait beaucoup.
Au fil du temps, ce mot a commencé à être utilisé dans des disciplines totalement différentes - en philosophie, en politique, en économie, en algèbre et en géométrie. Mais l'interprétation la plus simple de l'intégrale est donnée par les mathématiques.
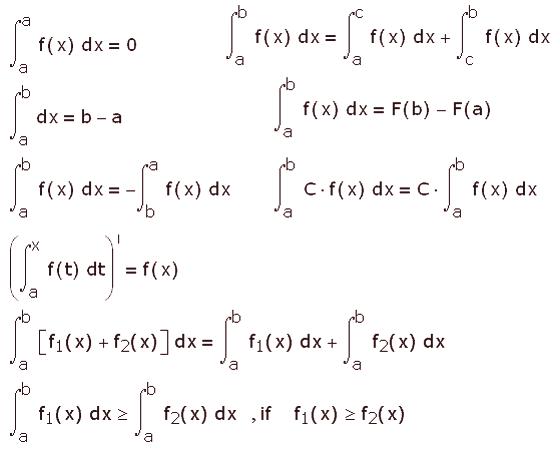
Certaines intégrales
Donc, l'intégrale est une certaine somme de parties séparées. Voici les exemples les plus simples pour une compréhension plus claire de l'essence de ce terme:
- Le sujet est l'intégrale (somme) des molécules.
- Une feuille dans une cellule est une intégrale (somme) de cellules.
- Le système solaire est l'intégrale (somme) du soleil et des planètes.
- La société fait partie intégrante des personnes.
- Un segment est l'intégrale (somme) des mètres. Si un petit segment, puis centimètres, millimètres ou segments microscopiques.
- régionToute surface est une intégrale de mètres carrés, de centimètres carrés ou de millimètres, ainsi que de zones microscopiques.
- Le volume est l'intégrale de mètres cubes ou, comme on l'appelle aussi, de litres.
Que sont les intégrales définies et indéfinies?
Commençons par un certain, car sa signification est plus facile à comprendre.
La géométrie étudie les zones . Par exemple, si vous souhaitez coller du papier peint à la maison, vous devez connaître la zone des murs pour déterminer la quantité de papier peint à acheter. Ensuite, il vous suffit de multiplier la longueur du mur par la hauteur pour obtenir sa surface. Dans ce cas, cette zone est une intégrale de mètres carrés ou de centimètres, en fonction des unités dans lesquelles vous l'avez mesurée. Mais les surfaces dont nous devons calculer l'aire n'ont pas toujours la forme d'un rectangle, d'un carré ou même d'un cercle. Dans la plupart des cas, ce sont des formes complexes avec des côtés ondulés. L'exemple le plus courant est l'aire d'une figure sous une courbe qui a l'équation y = 1 /x. Le fait est qu'il est impossible de trouver son aire à l'aide de formules ordinaires, par lesquelles on trouve l'aire d'un carré, d'un cercle ou même d'une sphère. À cette fin, une intégrale définie a été développée.
L’essence de la méthode est que notre figure complexe doit être divisée en rectangles très étroits, si étroits que la hauteur de deux adjacents est presque égale. Il est clair qu’en réalité, il est possible de réduire l’épaisseur de ces rectangles à l’infini, la taille dx est donc utilisée pour désigner leur épaisseur. X est la coordonnée et le préfixe d estdésignation de valeur décroissante infiniment. Par conséquent, lorsque nous écrivons dx - cela signifie que nous prenons un segment le long de l’axe des x dont la longueur est très petite, presque nulle.
Nous avons donc déjà convenu que la surface d’un chiffre correspond à l’intégrale de mètres carrés ou de tout autre chiffre comportant des surfaces plus petites. Alors, notre figure, dont nous cherchons la surface, est l’intégrale ou la somme de ces rectangles infiniment minces en lesquels nous l’avons divisée. Et sa superficie est la somme de leurs zones. En d’autres termes, notre tâche consiste à déterminer l’aire de chacun de ces rectangles, puis à les additionner - c’est une intégrale définie.
Parlons maintenant de l'intégrale indéfinie. Juste pour comprendre ce que c'est, vous devez d'abord en savoir plus sur le dérivé. Alors commençons.
La dérivée est l'angle d'inclinaison de la tangente à un graphique à un moment donné. En d'autres termes, la dérivée est la mesure dans laquelle le graphique est incliné à un endroit donné. Par exemple, une ligne droite en un point quelconque a la même pente et la courbe est différente, mais elle peut être répétée. Pour calculer la dérivée, il existe des formules spéciales et son processus de calcul s'appelle différenciation. C'est à dire la différenciation est la détermination de l'angle du graphe en un point donné.

Tableau des intégrales de base indéfinies
Et pour faire le contraire - pour trouver la formule du graphique par son angle d’inclinaison, ils ont recours à une opération d’intégration, ou sommation de données sur tous les points. Intégration et différenciationdeux processus réciproque. Seulement ici, ils utilisent non pas l'intégrale, qui se trouvait dans le premier paragraphe (pour déterminer la surface), mais l'autre - l'indéfini, c'est-à-dire sans limite.
Supposons que nous sachions que la dérivée d'une certaine fonction est égale à 5. 5 est l'angle d'inclinaison du graphique par rapport à l'axe des x en un point donné. Ensuite, en intégrant la dérivée, nous apprenons que la fonction de cette dérivée, également appelée primitive, est y = 5x + c, où c est un nombre quelconque. Pour l'intégration, ainsi que pour la différenciation, il existe des formules spéciales que l'on peut trouver dans les tableaux.
Conclusion
En conclusion, nous résumons le fait que la principale différence entre une intégrale définie et une intégrale indéfinie réside dans leurs assignations. Certaines intégrales sont utilisées pour calculer des paramètres liés, tels que l'aire, la longueur ou le volume, et indéfinis, lors du calcul de paramètres sans limites, c'est-à-dire de fonctions.
Vidéo intéressante sur ce sujet:







